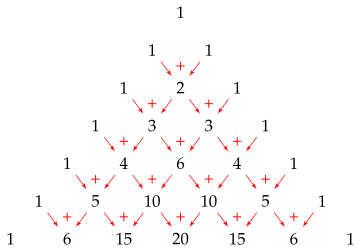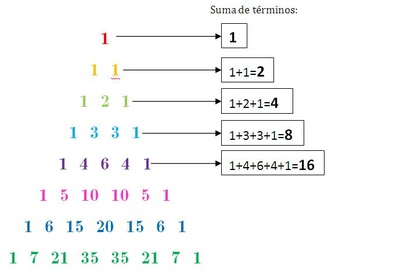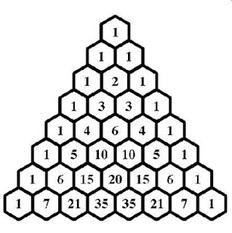
El triángulo de Pascal es un triángulo de números enteros, infinito y simétrico. Se empieza con un 1 en la primera fila, y en las filas siguientes se van colocando números de forma que cada uno de ellos sea la suma de los dos números que tiene encima. Se supone que los lugares fuera del triángulo contienen ceros, de forma que los bordes del triángulo están formados por unos. Aquí sólo se ve una parte; el triángulo continúa por debajo y es infinito.
El Triángulo de Pascal o Tartaglia tiene un origen, como en muchos otros casos, muy anterior al de estos dos matemáticos . Se tienen referencias que datan del siglo XII en China. De hecho, algunas de sus propiedades ya fueron estudiadas por el matemático chino Yang Hui (siglo XIII), así como el poeta persa Omar Khayyam (siglo XII).
El que se le asocie el nombre del filósofo, matemático Pascal (1623-1662) se debe a que el francés escribió el primer tratado sobre el triángulo. Lo de Tartaglia (1500-1557) viene porque el italiano fue de los primeros que lo publicaron en Europa.
El triángulo permite realizar diferentes operaciones matemáticas a partir de su conformación, las más básicas parten de la suma, pero se pueden trabajar desde series, el binomio de Newton y la serie de Fibonacci entre otras.
El que se le asocie el nombre del filósofo, matemático Pascal (1623-1662) se debe a que el francés escribió el primer tratado sobre el triángulo. Lo de Tartaglia (1500-1557) viene porque el italiano fue de los primeros que lo publicaron en Europa.
El triángulo permite realizar diferentes operaciones matemáticas a partir de su conformación, las más básicas parten de la suma, pero se pueden trabajar desde series, el binomio de Newton y la serie de Fibonacci entre otras.
Objetivos a conseguir:
- Obtener los números naturales.
- Asignar probabilidades en distribuciones binomiales.
- Obtener los números primos, pares, triangulares, cuadrados, hexagonales.
- Obtener diferentes series y sucesiones como la de Fibonacci.
- Obtener fractales.